

백준 1504 문제는 다익스트라 알고리즘을 이용해서 최단 경로를 찾는 문제다. 하지만 기본적인 다익스트라와 차이점은 양방향 그래프라는 점과 반드시 지나야 하는 정점이 주어진다는 것이다. 문제의 입력 예제에서는 정점 2와 정점 3을 반드시 지나는 조건을 충족하는 다익스트라 알고리즘을 요구하고 있다. 만약 다익스트라 알고리즘이 처음이라면 반드시 아래 글을 먼저 참고해서 이해하고 오길 바란다.
백준 1753 자바 최단거리 다익스트라 알고리즘 시간복잡도 JAVA
백준 1753 최단거리 문제는 다익스트라 알고리즘을 사용해서 풀어보는 문제다. 우선순위 큐를 사용해야 하고, 인접한 그래프의 방향성이 존재하는 그래프의 정보가 입력값으로 주어진다. 최단거
incomeplus.tistory.com
문제 시각화
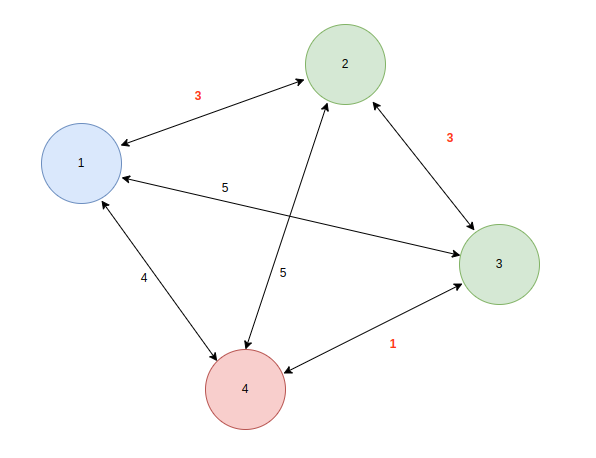
입력 예제를 시각화 해보면 다음 그래프를 그려볼 수 있다. 정점 2와 정점 3을 지나는 경로는 3+ 3+ 1 =7의 cost를 가지게 된다. 또한 방향성이 없는 양방향 그래프이기 때문에 모든 수를 고려하더라도 최단거리 cost는 7이 나온다.
문제 단순화
반드시 지나야 하는 정점이 있다는 걸 처음 생각하면 복잡하게 느껴질 수 있다. 알고리즘 문제는 항상 쪼갤 수 있을 만큼 쪼개서 생각하면 답이 나온다. 이 문제에서도 1->2->3->4로 가는 문제를 2개의 경우로 나누는 것이다. 1->2->3->4와 1->3->2->4 두가지 경우를 비교해서 cost가 적은 경로를 찾는다.
문제에서는 정점이 2개가 주어지게 되므로, 정점 1에서 반드시 지나야 하는 간선까지의 거리를 재고, 해당 정점에서 4번 까지 가는 cost를 비교하면 문제의 답을 찾을 수 있다.
백준 1504 문제풀이 자바
전역변수에 정점, 간선의 갯수를 정의해준다. 반드시 지나야 하는 정점 S1과 S2를 정의해준다. graph 2차원 배열을 담을 2차원 ArrayList를 정의한다. cost를 담을 Counter 배열을 정의한다. 마지막으로 무한으로 빠지는 걸 방지하기 위한 INF(INFINITE) 값은 200,000,000을 할당해줬다. 왜냐하면 간선의 최대수가 200,000이고 정점간 거리의 최대가 1000이기 때문이다.(200,000 x 1000 = 200,000,000)
public static int N, E; // 정점, 간선
public static int S1, S2;
public static ArrayList<ArrayList<Node>> graph; // 2차원 배열 생성
public static int[] counter;
public static final int INF = 200000000;
먼저 각 정점의 번호와 cost를 담을 클래스를 생성한다.
static class Node{
int idx, cost;
public Node(int idx, int cost){
this.idx = idx;
this.cost = cost;
}
}
다익스트라 알고리즘을 구현해줄 메소드를 구현한다. 출발점과 도착점을 매개변수로 받아서 cost를 반화하는 간단한 메소드다. cost를 담을 counter 배열을 IntegerMax값으로 초기화 해주고, PriorityQueue에 첫번째 정점과 cost 0을 담는다. 시작점에서 각 정점까지 도달하는 모든 경우를 구한 후 도착점의 cost값을 반환한다.
public static int trace(int start, int end){
// 정점 카운터 초기화
counter = new int[801];
// 정점 카운터에 Integer 맥스값 초기화
for(int i=0; i<N+1; i++){
counter[i] = Integer.MAX_VALUE;
}
// 우선순위 큐 생성
PriorityQueue<Node> queue = new PriorityQueue<Node>((o1, o2) -> Integer.compare(o1.cost, o2.cost));
// 출발점 queue에 추가
queue.offer(new Node(start, 0));
// 초기 노드 counter는 0으로 초기화
counter[start] = 0;
while(!queue.isEmpty()){
// 큐에서 Node 인스턴스를 추출
Node temp = queue.poll();
// temp.idx 정점까지 가는 cost가 작으면 해당 로직은 뛰어넘음.
if(counter[temp.idx] < temp.cost){
continue;
}
// 특정 정점까지 가기 위한 최단거리 구하는 로직
for(int i=0; i<graph.get(temp.idx).size(); i++){
Node nextNode = graph.get(temp.idx).get(i);
if(counter[nextNode.idx] > temp.cost + nextNode.cost){
counter[nextNode.idx] = temp.cost + nextNode.cost;
queue.offer(new Node(nextNode.idx, counter[nextNode.idx]));
}
}
}
return counter[end];
}
입력값들을 받아서 정점과 간선의 갯수, 각 정점의 cost를 입력받는다. 해당 문제는 양방향 그래프를 구현해야 하므로, graph 2차원 배열에 두가지 형태의 클래스 인스턴스를 생성해서 추가해준다.
Scanner in = new Scanner(System.in);
N = in.nextInt();
E = in.nextInt();
// 그래프 초기화 진행
graph = new ArrayList<ArrayList<Node>>();
// 그래프 노드 초기화
for(int i=0; i<N+1; i++){
graph.add(new ArrayList<Node>());
}
// 노드의 cost와 번호로 2차원 그래프에 초기화
for(int i=0; i<E; i++){
int u = in.nextInt();
int v = in.nextInt();
int w = in.nextInt();
// 양방향 그래프 구현
graph.get(u).add(new Node(v, w));
graph.get(v).add(new Node(u, w));
반드시 거쳐야 하는 정점은 2개가 주어진다. 정점을 지나는 최단 경로의 경우의 수는 2가지를 비교하면 된다. 리턴값은 각 케이스들 모두 INF 보다 작아야 하며 케이스 1과 케이스 2 중 작은 값을 리턴값으로 할당한다.
// 반드시 거쳐야 하는 두개의 정점
S1 = in.nextInt();
S2 = in.nextInt();
int path1 = trace(1,S1);
int path2 = trace(S1,S2);
int path3 = trace(S1,N);
int path4 = trace(S2,N);
int path5 = trace(1,S2);
int case1 = path1+path4+path2; //4
int case2 = path5+path3+path2; //10
int ans = (case1 >= INF && case2 >= INF) ? -1 : Math.min(case1, case2);
System.out.println(ans);
백준 1504 자바 Code
/*
Owner : Developer Blog
Title : 특정한 최단 경로
Algorithm : 다익스트라 알고리즘
Date : 2022-04-05
*/
import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.Scanner;
public class A_1504 {
static class Node{
int idx, cost;
public Node(int idx, int cost){
this.idx = idx;
this.cost = cost;
}
}
public static int N, E; // 정점, 간선
public static int S1, S2;
public static ArrayList<ArrayList<Node>> graph; // 2차원 배열 생성
public static int[] counter;
public static StringBuilder sb = new StringBuilder();
public static final int INF = 200000000;
public static int trace(int start, int end){
// 정점 카운터 초기화
counter = new int[801];
// 정점 카운터에 Integer 맥스값 초기화
for(int i=0; i<N+1; i++){
counter[i] = Integer.MAX_VALUE;
}
// 우선순위 큐 생성
PriorityQueue<Node> queue = new PriorityQueue<Node>((o1, o2) -> Integer.compare(o1.cost, o2.cost));
// 출발점 queue에 추가
queue.offer(new Node(start, 0));
// 초기 노드 counter는 0으로 초기화
counter[start] = 0;
while(!queue.isEmpty()){
// 큐에서 Node 인스턴스를 추출
Node temp = queue.poll();
// temp.idx 정점까지 가는 cost가 작으면 해당 로직은 뛰어넘음.
if(counter[temp.idx] < temp.cost){
continue;
}
// 특정 정점까지 가기 위한 최단거리 구하는 로직
for(int i=0; i<graph.get(temp.idx).size(); i++){
Node nextNode = graph.get(temp.idx).get(i);
if(counter[nextNode.idx] > temp.cost + nextNode.cost){
counter[nextNode.idx] = temp.cost + nextNode.cost;
queue.offer(new Node(nextNode.idx, counter[nextNode.idx]));
}
}
}
return counter[end];
}
public static void main(String[] args){
Scanner in = new Scanner(System.in);
N = in.nextInt();
E = in.nextInt();
// 그래프 초기화 진행
graph = new ArrayList<ArrayList<Node>>();
// 그래프 노드 초기화
for(int i=0; i<N+1; i++){
graph.add(new ArrayList<Node>());
}
// 노드의 cost와 번호로 2차원 그래프에 초기화
for(int i=0; i<E; i++){
int u = in.nextInt();
int v = in.nextInt();
int w = in.nextInt();
// 양방향 그래프 구현
graph.get(u).add(new Node(v, w));
graph.get(v).add(new Node(u, w));
}
// 반드시 거쳐야 하는 두개의 정점
S1 = in.nextInt();
S2 = in.nextInt();
int path1 = trace(1,S1);
int path2 = trace(S1,S2);
int path3 = trace(S1,N);
int path4 = trace(S2,N);
int path5 = trace(1,S2);
int case1 = path1+path4+path2; //4
int case2 = path5+path3+path2; //10
int ans = (case1 >= INF && case2 >= INF) ? -1 : Math.min(case1, case2);
System.out.println(ans);
}
}
백준 1504 자바 제출결과
메모리가 314MB, 시간은 1.5초 가량 소요되었다. 다익스트라 알고리즘이 최단경로를 찾으면서 모든 경로를 고려하다 보니 리소스가 많이 투입된 것으로 보인다.

더 많은 콘텐츠
백준 1707 자바 이분 그래프 판별 알고리즘
백준 1707 이분 그래프 판별 알고리즘 백준 1707 이분 그래프 판별 문제를 풀기 위해서는 먼저 '이분 그래프'에 대해서 이해해야 한다. 그래프 자료구조는 비선형 자료구조에 속한다. 즉 자료들이
incomeplus.tistory.com
'Programming > Algorithm' 카테고리의 다른 글
| 백준 1753 자바 최단거리 다익스트라 알고리즘 시간복잡도 JAVA (0) | 2022.03.24 |
|---|---|
| 백준 1707 자바 이분 그래프 판별 알고리즘 (0) | 2022.03.23 |
| 백준 7562 나이트의 이동 자바 알고리즘 java 풀이 (0) | 2022.03.22 |
| 백준 1697 숨바꼭질 문제 자바 JAVA BFS 알고리즘 풀이 (1) | 2022.03.12 |
| 백준 7569 토마토 3D 알고리즘 문제 자바 JAVA 풀이 해설 리뷰 (0) | 2022.03.11 |
| 백준 7576 토마토 알고리즘 문제 자바 JAVA CODE (0) | 2022.03.11 |





댓글