
선형회귀분석과 다르게, 참과 거짓만을
분별해야 하는 모델이 필요하다. 우리는
이때 로지스틱 회귀 분석 알고리즘을
이용하게 된다.
로지스틱 회귀 분석
참, 거짓을 구분하는 알고리즘이
로지스틱 회귀 Logistic Regression이다.
로지스틱 회귀는 선형회귀와 동일하게
선을 그어나가는 알고리즘이다. 하지만
참 / 거짓 둘중 하나를 판별해야 하기
때문에, 그래프가 선형회귀와는 다른
모양을 가진다.로지스틱 회귀 Logistic Regression

0과 1 사이에서 그려지는 그래프를
가능하게하는 함수가 시그모이드 함수다.
시그모이드(Sigmoid) 함수
시그모이드 함수 공식은 다음과 같다.
우리가 사용해야 하는 공식은 결국
ax+b인 1차 방정식이다.

오차를 줄이기 위해서 learning-rate를
조정하지만, 기울기 a가 커지면, 기울기가
급격하게 올라가고, b가 커지면 그래프
자체가 크게 움직인다.
오차를 줄이기 위해서는 선형회귀와
동일하게 경사 하강법을 사용한다. 여기서
주의할 점은 시그모이드 함수는 종속변수
y값이 무조건 0과 1 사이에 존재한다는 것이다.
y의 실제값이 0일 때 예측값이 1로 가면
오차값은 무한히 커져야 한다.
반대로, y의 실제값이 1일 때 예측값이 0으로 가면
오차값은 무한히 커져야 한다.
이걸 가능하게 해주는 함수가 로그함수다.
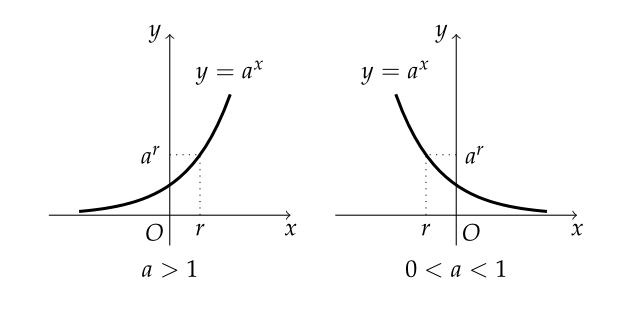
로지스틱 회귀 코드 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
import tensorflow as tf
import numpy as np
tf.compat.v1.disable_eager_execution()
# 데이터를 셋팅합니다.
data = [[2, 0],[4, 0],[6, 0],[8, 1],[10, 1],[12, 1],[14, 1]]
x_data = [x_row[0] for x_row in data]
y_data = [y_row[1] for y_row in data]
# a, b값 변수를 설정합니다..
a = tf.Variable(tf.compat.v1.random_normal([1], dtype=tf.float64, seed=0))
b = tf.Variable(tf.compat.v1.random_normal([1], dtype=tf.float64, seed=0))
# 시그모이드 함수의 방정식을 세운다.
y = 1/(1+np.e**(a*x_data+b))
# 평균제곱근 오차사용
loss = -tf.compat.v1.reduce_mean(np.array(y_data) * tf.compat.v1.log(y) + (1-np.array(y_data)) * tf.compat.v1.log(1-y))
# 학습률 값
learning_rate = 0.5
# 경사하강법 사용합니다.
gradient_descent = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(loss)
# 학습
with tf.compat.v1.Session() as sess:
# 변수 초기화
sess.run(tf.compat.v1.global_variables_initializer())
for i in range(60000):
sess.run(gradient_descent)
if i % 1000 == 0:
print("Epoch: %.f, loss=%.4f, 기울기 a=%.4f, y 절편=%.4f" % (i, sess.run(loss), sess.run(a), sess.run(b)))
|
cs |
다중 로지스틱 회귀
독립변수가 1개면 계산하기가 편하겠지만,
여러가지 변수가 종합적으로 작용해서
종속변수 y의 값을 결정하는 것이 현실에
더 맞는 경우다.
독립변수 x가 추가되면 기울기 a값도 추가하고,
이를 계산하기 위해서는 행렬을 사용해서
결과값을 도출해낼 수 있다.
코드 구현
일반 로지스틱 회귀와는 다르게, 변수를 담는 공간을
placeholder에 담는다. placeholder는 입력값을
저장하는 컨테이너의 개념이다.
사용방법 : placeholder('데이터형', '행렬의 차원', '이름')
tensorflow.cast()함수를 사용해서,
y값이 0.5이 되도록 학습을 진행한다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 | import tensorflow as tf import numpy as np tf.compat.v1.disable_eager_execution() # 실행할 때마다 같은 결과를 출력하기 위한 seed값 설정 seed = 0 np.random.seed(seed) tf.compat.v1.set_random_seed(seed) # x, y의 데이터 값 x_data = np.array([[2,3],[3,4],[6,4],[8,6],[10,7],[12,8],[14,9]]) y_data = np.array([0,0,0,1,1,1,1]).reshape(7,1) # 입력 값을 플레이스 홀더에 저장한다. X = tf.compat.v1.placeholder(tf.float64, shape=[None, 2]) Y = tf.compat.v1.placeholder(tf.float64, shape=[None, 1]) # 기울기 a와 바이어스 b의 값을 임의로 정한다. a = tf.Variable(tf.compat.v1.random_uniform([2,1], dtype=tf.float64)) b = tf.Variable(tf.compat.v1.random_uniform([1], dtype=tf.float64)) # y 시그모이드 함수의 방정식을 세운다. y = tf.sigmoid(tf.matmul(X, a) + b) # 평균 제곱근 오차 사용해서 오차를 추적한다. loss = -tf.reduce_mean(Y * tf.compat.v1.log(y) + (1 - Y) * tf.compat.v1.log(1 - y)) # 학습률 값을 지정한다. learning_rate = 0.1 # 경사 하강법 사용 gradient_descent = tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(loss) predicted = tf.cast(y > 0.5, dtype=tf.float64) accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float64)) # 학습을 진행한다. with tf.compat.v1.Session() as sess: sess.run(tf.compat.v1.global_variables_initializer()) for i in range(10000): a_, b_, loss_, _ = sess.run([a, b, loss, gradient_descent], feed_dict={X:x_data, Y:y_data}) # if (i+1) % 300 == 0: # print("step=%d, a1=%.4f, a2=%.4f, b=%.4f, loss=%.4f" % (i+1, a_[0], a_[1], b_, loss_)) # 실제값 적용으로 예측값 구하는 방법 # 7시간 공부하고 6시간 과외받은 학생의 점수는? new_x = np.array([14,5]).reshape(1,2) new_y = sess.run(y, feed_dict={X:new_x}) print("공부한 시간 : %d, 과외 수업 횟수 : %d" % (new_x[:,0], new_x[:, 1])) print("합격 가능성 : %6.2f %%" % (new_y*100)) | cs |
더 읽을거리
딥러닝 머신러닝 차이, 머신러닝 딥러닝
머신러닝 딥러닝 차이 알파고가 대한민국을 초토화 시킨지 5년이 지났다. 실생활에도 인공지능이 많이 들어 왔고, 무수히 쌓여가는 데이터들을 기반으로 한 새로운 사업들이 계속 등장하고 있
incomeplus.tistory.com
딥러닝 기본 구조 이해하기 2
딥러닝 기본구조 딥러닝의 근간을 이루는 것은 인공 신경망이라고 불리는 작은 연산장치들의 집합이다. 신경망의 뼈대는 알고리즘에 많은 의존도를 보인다. 그 중 가장 대표적인 것이 선형 회
incomeplus.tistory.com
딥러닝 머신러닝 인공지능 경사 하강법 10분만에 이해하기 쫄지마 딥러닝
딥러닝 경사 하강법? 이전 글에서 살펴본 선형회귀에서 오차를 줄여나가면서 예측값을 수정한다고 했다. 선형회귀에서 a값과 b값을 조정하면서 오차를 줄여나가게 되는데, 만약 기울기 a를 너무
incomeplus.tistory.com
'Programming > MachineLearning' 카테고리의 다른 글
| 딥러닝 실제 모델 만드는 방법 딥러닝 코드 구현해보기 이항 분류 keras 모듈 이용하기 (feat 인디언 당뇨병 문제) (0) | 2021.12.15 |
|---|---|
| 딥러닝 오차 역전파 10분만에 이해하기 (0) | 2021.12.15 |
| 딥러닝 핵심 개념 신경망 10분만에 이해하기 (0) | 2021.12.15 |
| 딥러닝 머신러닝 인공지능 경사 하강법 10분만에 이해하기 쫄지마 딥러닝 (0) | 2021.12.15 |
| 딥러닝 기본 구조 이해하기 선형회귀 , 평균 제곱근 오차 10분만에 이해하기 (0) | 2021.12.15 |
| 딥러닝의 층 구조 딥러닝을 배워보자 (0) | 2021.12.15 |





댓글